Mathématiques & miracles : Le paradoxe de Banach-Tarski

Les mathématiques ont cette étrange capacité à révéler des vérités qui défient notre intuition. L’une d’elles, le paradoxe de Banach-Tarski, introduit pour résoudre des questions fondamentales sur la théorie de la mesure. Il a eu un impact plus significatif sur la théorie des groupes, où il a été le point de départ pour le développement de la théorie des groupes amenables. Explorons ce paradoxe, en nous basant sur l'article du Prof. Volker Runde: 'The Banach-Tarski paradox or What mathematics and miracles have in common' tout en établissant des parallèles avec le recit biblique sur la multiplication des pains.

Paradoxe de Banach-Tarski

Le paradoxe de Banach-Tarski est un résultat fascinant de la théorie des ensembles démontrant qu'il est possible de diviser une boule unitaire dans R3 en un nombre fini de pièces et de les réorganiser par isométrie pour former deux boules unitaires identiques à la première: Pas de mesure finiment additive sur R3 qui soit définie sur chaque sous-ensemble de R3, invariante à l'isométrie et qui donne à la boule unitaire une mesure non nulle. En fait, l'idée de conservation du volume ne s'applique qu'aux ensembles mesurables de Lebesgue ou 'Lp spaces'. Par conséquent, on ne peut pas étendre la mesure de Lebesgue à tous les sous-ensembles de R3 ; c'est-à-dire qu'il existe des ensembles non mesurables par Lebesgue, des ensembles pour lesquels l'idée de volume ne s'applique pas.

• Analogie:

Imaginez une boule, disons une 'orange'. Le paradoxe de Banach-Tarski affirme qu’on peut la couper en quelques morceaux très particuliers, les déplacer et les tourner, pour obtenir deux oranges identiques à la première. Pas une goutte de jus en plus ou en moins ! Cela semble impossible : où est donc passée la conservation du volume ? La réponse réside dans la nature étrange de ces morceaux. Ils sont si abstraits qu’on ne peut pas leur donner une taille classique. On les appelle des "ensembles non mesurables". Ce tour de magie ne marche qu’en trois dimensions (pas en 2D ou 1D) et repose sur une règle spéciale: 'l’axiome du choix (axiome parfois considéré comme controversé).

Banach-Tarski paradox -> 'Axiome du choix + transformations du groupe des mouvements euclidiens SO(3)'.

• Casuistique:

C'est un théorème si complexe que même s'il nous était facile de construire une isométrie (une bijection de X à X qui préserve la distance), bijection entre une & deux sphères (deux ensembles infinis ressemblant à un continuum), il nous serait très difficile de concevoir un moyen pour fractionner la sphère en plusieurs morceaux et dknc utiliser le 'Mouvement Géométrique' pour construire deux sphères à partir d'elle. En permettant l'utilisation de l'Axiome de choix, nous pouvons obtenir des ensembles qui seront si compliqués qu'on ne pourrait pas leur attribuer une mesure compatible avec les propriétés souhaitées.

Nous ne pouvons pas diviser un cercle en nombre fini de pièces et en construire deux cercles, de nouveau. Car la plupart des ensembles que nous pouvons construire sont non-mesurables. (Théoriquement, certaines partitions ne sont pas mesurables sur le plan Lebesgue. Mais, il est possible de le faire avec un nombre infini dénombrable de pièces. Il y a quelque chose dans la nature des mouvements géométriques en 3D qui le rend possible..

Ainsi, le paradoxe Banach-Tarski ne double pas le volume de la balle parce que les pièces de la décomposition ne peuvent pas se voir attribuer un volume. Une sphère n'existe que sous la forme d'un ensemble infini de points dans notre imaginaire, et en réalité. Une telle beauté n'existe que dans le domaine des mathématiques.

• Corollaire:

Ce phénomène, rendu possible par l’existence de sous-ensembles paradoxaux et l’absence de mesure invariante dans des espaces tridimensionnels, pourrait trouver une résonance inattendue dans le principe de l’Énergie Libre de l’Inférence Active où les systèmes vivants, minimisent l'incertitude, via des structures complexes comme une couverture de Markov évoluant dans un groupe de Lie exceptionnel à 248 dimensions, tel le groupe E8. Et sur le plan spirituel, ce paradoxe évoque le miracle de la multiplication des pains par Jésus, où cinq pains et deux poissons ont nourri une multitude, reflétant une interconnexion divine entre matière, énergie et information, semblable au réseau d’Indra. Ainsi, ce paradoxe pourrait être une clé mathématique pour comprendre l’infini dans le fini, un écho à la providence divine et à l’abondance spirituelle du Royaume des Cieux.

Axiome du choix

Cet axiome indique que compte tenu de toute collection d'ensembles non vides, il est possible de choisir un élément dans chaque ensemble, même si la collection est infinie: Propriété de caractère aléatoire qui est indécidable -- car la valeur du caractère aléatoire est fortement liée à la taille des ensembles. Nous pourrions savoir qu'elle existe, nous savons que la valeur est en [0,1], mais nous ne la trouverons peut-être jamais. Bien que cela puisse sembler intuitif, ses implications sont si profondes, conduisant à des résultats défiant le bon sens.

• Simulation conceptuelle de l'Axiome du choix

Pour illustrer l'axiome du choix & son rôle dans le paradoxe Banach-Tarski, envisagez le défi de sélectionner un élément parmi un nombre infini d'ensembles. Pour les collections finies, le processus est simple: nous choisissons simplement un élément dans chaque ensemble. Cependant, pour les collections infinies, l'axiome du choix garantit l'existence d'une fonction de sélection, même si nous ne pouvons pas la construire explicitement dans tous les cas.

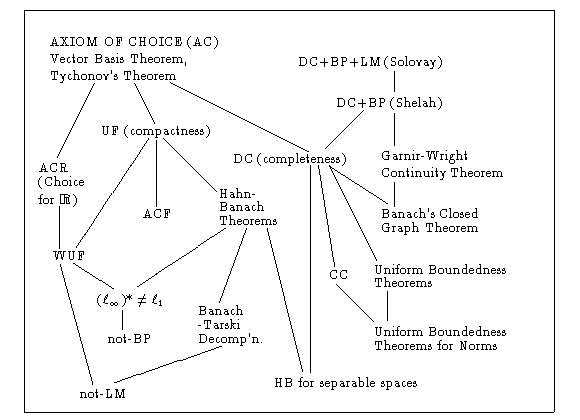
Dans le contexte du paradoxe Banach-Tarski, l'axiome du choix est utilisé pour sélectionner des points d'une sphère de manière à ce que la sphère puisse être décomposée en un nombre fini d'ensembles non mesurables. Ces ensembles ne peuvent pas se voir attribuer un volume significatif, ce qui permet le remontage paradoxal en deux sphères identiques. Mais ce n'est pas le seul tour que peuvent nous jouer les ensembles non mesurables, ces objets mathématiques un peu étranges qui ne rentrent pas dans le cadre habituel de la mesure.

• Le Cercle au Carré, version non mesurable: Oubliez la règle & le compas, on ne cherche plus à construire un carré de même aire qu'un cercle donné. Ici, la question est: "Peut-on découper le cercle en un nombre fini de morceaux qui, une fois déplacés, forment un carré de même aire ?" Attention, les morceaux obtenus sont non mesurables!

• Le Problème continu des quatre couleurs: Un puzzle classique : peut-on colorier chaque point du plan en utilisant seulement quatre couleurs, de manière à ce que deux points à une distance d'une unité (un mètre, un centimètre, peu importe !) ne soient jamais de la même couleur ? On sait facilement que trois couleurs ne suffisent pas, et il est un peu plus difficile de montrer que sept couleurs sont suffisantes. La théorie actuelle penche vers une réponse affirmative pour le problème continu des quatre couleurs, mais en utilisant des ensembles non mesurables pour définir chaque couleur.

Ces exemples nous montrent que la notion d'ensemble mesurable n'est pas toujours nécessaire en géométrie. Les ensembles non mesurables, bien que contre-intuitifs, nous permettent de résoudre des problèmes classiques de manière inattendue.

Un écho biblique: La multiplication des pains

Dans l’Évangile de Matthieu (14:14-21), Jésus nourrit plus de cinq mille personnes avec cinq pains et deux poissons. Une quantité finie devient infinie, défiant toute logique. Le parallèle avec Banach-Tarski est frappant: une boule devient deux, un pain devient des milliers. Les deux histoires nous invitent à dépasser notre compréhension habituelle du "combien" et à plonger dans un mystère plus grand, qu’il soit mathématique ou divin.

Pour simplifier, on peut imaginer un "pain" unidimensionnel comme un segment de ligne I = [0, 1], l'intervalle de 0 à 1. Étirons I en utilisant la fonction f(x) = 3x, de sorte que J = f(I) = [0, 3]. Retirons ensuite le tiers médian, laissant deux "pains" identiques, à savoir [0, 1] et [2, 3]. Ce processus peut être répété et généralisé en 3D, permettant de générer autant de "pains" que nécessaire.

Cependant, ce modèle pose quelques problèmes : tout est étiré linéairement, si bien que la structure atomique du "pain" ressemble désormais à celle d'un monde fantastique visité par Gulliver, avec des proportions démesurées. Si l'on utilise une fonction d'étirement non linéaire f pour préserver la structure atomique, alors aucune augmentation de masse ne se produit, et f va sûrement déchirer les fibres du "pain" de sorte qu'il ne restera rien de reconnaissable comme nourriture.

• Contre-mesure:

Dans le monde physique, nous devons à un moment avoir des particules fondamentales et indivisibles. Sinon, nous serions en mesure de créer de la masse et de l'énergie ex-nihilo plutôt que de les réduire à néant si nous inversons le processus. Fondamentalement, il nous est impossible d'avoir ou de concevoir de la matière continue et un espace isotrope rigide (la symétrie de rotation échoue, même si nous optons pour les points de coordonnées localement ou globalement). D'ailleurs, l'abandon de l'isotropie au détriment de la 'continuité' traduit une différence de la théorie des ensembles.

Conceptualiser le paradoxe de Banach-Tarski, revient à comprendre les propriétés de volume des corps en trois dimensions. Prenons un cube et une sphère. Nous pouvons déplacer ces corps dans l'espace sans modifier leur volume. Cette propriété est essentielle pour comprendre les transformations impliquées dans le paradoxe.

Conclusion

Le paradoxe de Banach-Tarski et la multiplication des pains nous rappellent que certaines vérités dépassent notre imagination. L’un vit dans les équations, l’autre dans les Écritures, mais tous deux nous invitent à explorer l’infini. Bien plus qu’une bizarrerie, ce paradoxe constitue une mise en cause radicale de la théorie des ensembles elle-même, nous forçant à réévaluer les fondements de la mathématiques et à accepter que notre intuition, ancrée dans le mesurable, est fondamentalement inadéquate face à ces étranges vérités. Et si les mathématiques et les miracles partageaient un même mystère, caché juste sous la surface de notre réalité ?.